Nagoya City Science Museum

Purpose of Exhibition

Additional Knowledge

It is a German physicist, Ernst Chladni who discovered the way of generating these patterns.
Chladni began to study sound from the late 18th century.
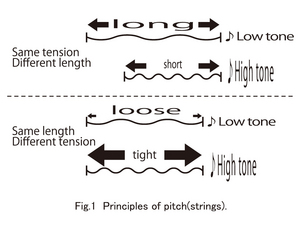
For stringed instruments such as violins and guitars, sound is emitted by vibrating strings.
The strings vibration can be expressed using trigonometric functions, as taught in high school physics. On the other hand, in the cases of timpani, drums, or Japanese drums, sound is generated by vibrating skin called "head" that is stretched over the large bowl.
Also, for stringed instruments such as violin and guitars, sound generated from the strings goes into the instrument body, turning into a deep sound. This body is also a surface. Compared with strings, mathematical expression of a vibrating surface is so complex that it can not be represented by a simple trigonometric function.
In case of sound generated by vibrating strings, the modification of the pitch is determined by the length of the stretched string, and the strength of the tension.
The shorter the string is, and the tighter it is pulled, the higher the pitch is. On the other hand, when a long string is loosened, the lower the sound is. When playing stringed instruments, you prepare the instrument by adjusting the tension of the strings.
The Timpani, unlike drums and Japanese drums, is capable of producing a proper musical scale.
The tension at the "head" of the timpani is modified by using six to eight screws. If not evenly extended, the pitch will not appear. Percussionists make adjustments while confirming a pitch with their ears.
In this exhibition, you can see the compexity of vibrating surface, that is a Chladni figure. With the timpani too, you can imagine percussionists have some difficulties when they tune timpanies.
If you have a chance to go to a orchestra concert, perk up your ear's on the sound of timpanies and their player.

Article by Tetsuro Ojio, curator