Nagoya City Science Museum
TOP > Exhibition Guide > Keyword Search > Starting with "M" > moment > Moment of Inertia
Moment of Inertia


Purpose of Exhibition
If we rotate two disks of the same size and the same weight on a slope, each speed differs. The difference between the two disks is the positioning in which the weights are installed inside the disks. We would like you to think about why that happens.
Additional Knowledge
[The differences between the disks]
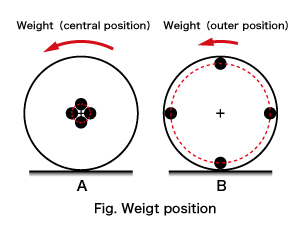
You can get the two disks, disk A and disk B to compete, rotating using a slope. The shape and the weight and the size of the disks are just the same. The difference is in the positioning of weight distribution in the weights. The weight of A is gathered in the center of the disk while the weight of B is installed in the peripheral part.
[Energy when rotation falls]
It is the rotation of A, with its weight gathered in the center of the disk, which falls on the slope first if the two rotate together until the goal and the rotation falls. In other words, to accelerate in the same way, at the same speed, suppose that the two fall to the goal at the same time. In short, it follows that the disks accelerate similarly, and pass through the goal at the same speed. At that time, disk B with its weight in the peripheral area has a larger amount of energy than the disk A in the center.
The reason is as follows. Even if the disks rotate at the same time and at the same speed, the one with the peripheral weight rotates faster than the disk with weight in the center. The faster movement generates a larger amount of energy. If the disk rotates at the same speed, the energy of the disk is larger because the disk with the weight in the periphery rotates faster.
[The reason why speed differs]
It is strange that one generates more energy at the goal than the other, even if the two rotate on the same slope.
In the case in which two disks with the same weight fall in the same distance, they must generate the same energy. In order to get rid of this contradiction, if the speed at which the two disks reach the goals differs, it is all right. If B reach the goal slower than A, it follows that the two disks generate the same energy respectively in reaching the goal.
In short, if the two disks compete, it is A that reaches the goal beforehand, B that comes next.
[Moment of Inertia]
As you can see in this experiment, it follows that even if disks are the same size and the same weight, if their weights are not balanced, the way of rotating is clearly different. To indicate the way of rotating simply, the physics of the "moment of inertia" is used. The moment of inertia is indicated by the addition of square of distance from the center of rotation and weights.
Article by Yoshitaka Yamada, curator
