Nagoya City Science Museum

Purpose of Exhibition

In nature, some phenomena can be presented in slightly distinctive numbers. The spiral structure of sunflower seeds, intricate coastlines and bee hives - - - what math is related to these?

Additional Knowledge

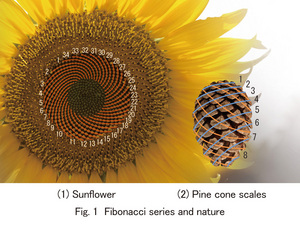
[Fibonacci Series]
The Fibonacci Series is a mathematical number patter where the first two numbers in the series are one and one. To obtain each number of the series, you simply add the two numbers that came before it. For example, the series goes 1,1,2,3,5,8,13,21 - - -Following are the Fibonacci series that can be observed in natural phenomena. In a sunflower, the arrangement of seeds is a whirlpool-like pattern. The number of the whirlpool's arms is the Fibonacci series. Other than that, pine cones and pineapple scales have whirlpool-like patterns, but the number of arms also demonstrates the Fibonacci series.
Fibonacci was a mathematician who played an important role in Pisa, Italy between the 12th and the 13th century. He introduced the Hindu-Arabic numeral system (the numbers from 0 to 9 familiar to us today) with a book called "The Book of Calculation" in Europe. In the book, he asked a question called "Question of Rabbits": how does a pair of rabbits reproduce under certain conditions? The answer is the Fibonacci series. The bigger the Fibonacci series gets, the closer the proportion of neighboring 2 numbers come to the fixed number, and the ultimate number (when the number is calculated over and over) is the golden proportion. The golden proportion is the most beautiful numerical proportion (Approximately 1:16).

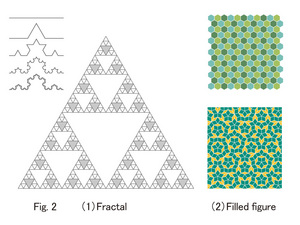
[Fractal]
As with a tree branch similar to the shape of the entire tree, and part of intricate coastlines similar to the bigger dimension of the coastline, Fractal can be observed on these occasions in which a part of a figure and the whole figure itself are similar. The term "Fractal" is named after a Latin word fractus meaning "broken" or "fractured" by a mathematician, Beno_t Mandelbrot（1924-2010）. It was presented in his thesis in 1977. Although Fractal is a mathematical concept and technically it does not exist in nature, as a frequently applied example it can be found in every part of the natural world, such as in the branch structure of the blood vessels, in human beings and animals, the structure of lungs and mountainous topography.

[Filled Figure]
Flat surfaces and open spaces can be filled with one or several kinds of figures and three dimensions. We can see these figures in natural objects. A beehive tightly arranged with regular hexagons is a typical example. Columnar joint in basalt is arranged tightly in a hexagonal form, too.
Except for hexagons, regular polygons, which can be filled with only one kind of flat surface, are only regular triangles and squares. If not regular polygons, there are many more figures such as parallelograms that can fill flat surfaces with only one kind. If there are polygons of many kinds, there is a variety, but each one is filled with periodic patterns. Besides the periodic patterns, there are also no periodically filled figures. An English mathematical physicist, Roger Penrose (born in 1931), discovered no periodic 2D figures with two kinds of figures. The figures are called Penrose style. It was considered that there was no such filled structure equivalent to the Penrose style in crystals of nature. However, crystals with a five point symmetry the same as the Penrose style were discovered in 1984, and they were named quasicrystal.

Article by Yoshitaka Yamada, curator