名古屋市科学館

展示作品の狙い

　円周率πや三平方の定理（ピタゴラスの定理）について図形を用いて理解してもらいます。

知識プラスワン

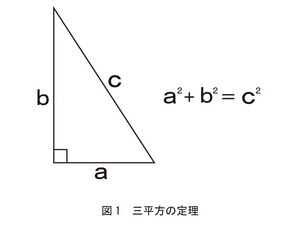
【三平方の定理】
　三平方の定理はピタゴラスの定理ともいわれ、「直角三角形の斜辺の平方は、他の二辺の平方の和に等しい。」というものです。ピタゴラスは古代ギリシャの数学者・哲学者ですが、三平方の定理はピタゴラスの時代よりも古くから知られており、なぜ彼の名前が付けられているのかよく分かっていません。古代バビロニアの粘土板に、三平方の定理を知っていたと考えられる記述と図形が残されています。
　三平方の定理は、日本では古くから鉤股弦の定理（こうこげんのていり）として知られていました。「三平方の定理」という呼び方は第二次世界対戦中に作られた呼び方です。
　三平方の定理の証明は数百種類あると言われ、現在でも新しい証明方法が考えだされたりしています。
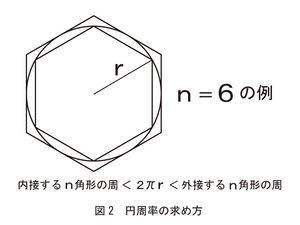
【円周率、π】
　円周率はギリシャ文字のπ（パイ）で表されます。円周の長さを直径で割った数です。どんな大きさの円でも円周と直径の比率が一定の値になることは紀元前から各地で知られており、正確な値を求める努力がなされてきました。古代ギリシャのアルキメデスが円に内接する多角形と外接する正多角形を用いて円周率を求め、その方法で後世の人々がより正確な円周率を求めていきました。もちろん、それ以外にも様々な計算方法が考え出され、円周率を求めるのに一生を捧げた人もいました。
　円周率の計算はコンピュータの性能を示すためにも用いられ、日本の数学者、金田康正氏によって円周率の記録が次々と塗り替えられていきました。