Nagoya City Science Museum
TOP > Exhibition Guide > Keyword Search > Starting with "M" > mathematics > Ruled Surface
Ruled Surface

Purpose of Exhibition
This exhibition introduces the possibility of creating a curved surface by arranging straight lines. It is easy to see a flat surface being produced by arranging straight lines in a row. But, there are some curved surfaces that do not look like they are produced by only straight lines.
Additional Knowledge
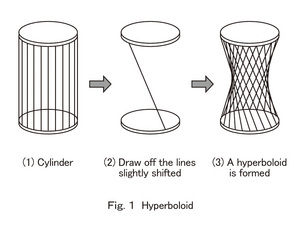
<Hyperbola>
A cylinder, which has a similar shape to a Japanese style tea leaf container, can be easily made of straight lines. Its body is made as you arrange straight lines vertically around the circle. The bottom and top of the cylinder look circular. In a cylinder, the lines connect the circle on top and at bottom vertically. Next, not drawing the lines straight down from the top circle, cross these straight lines down along to the circle at the bottom. Cross all the straight lines down. The shape should look just like a grid pattern. Now the body shape has changed and its middle part looks curved inward. The entire shape does not look like it is formed with only straight lines In the exhibit, not only are Hyperbola shapes presented but the change from a cylinder to Hyperbola can be observed. You can see that a Hyperbola is actually made with straight lines while observing threads one by one that consist of a Hyperbola.
A shape of the Hyperbola in the exhibit is technically named "One-Sheeted Circular Hyperbola".
Kobe Port Tower in the port of Kobe city, Hyogo Prefecture has the same shape. It is formed with straight pipes but the entire shape is a Hyperbola.
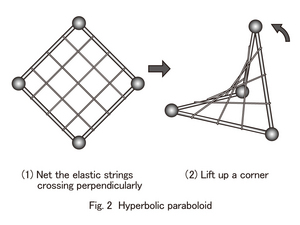
<Hyperbolic Parabola>
This is a board made up of vertical and horizontal lines. Cells of the board were replaced by rubber. Three corners of the board remain where they are, and just one corner is lifted straight up, so that the cells of the board that were flat become a curved surface.
However, the rubber will stretch, but rather than being slack, remains straight.
The finished surface is called a "hyperbolic parabola". In the exhibition, the transformational change from flat surface to hyperbolic parabola can be observed. Again, you can see that each rubber is not twisted. The soap bubble produced as the structure model in the exhibition and submerged into the liquid soap also has the same hyperbolic parabola presented in the exhibition.
Article by Yoshitaka Yamada, curator
